Semidirect product
Definition a remarks
We start with a proposition:
Proposition
Let $G$ be a group, $N$ a normal subgroup and $H$ a subgroup. The following are equivalent:
1. There exists a group homomorphism $\phi: G \rightarrow H$ such that $\phi|_H=id$ and $\mbox{Ker}(\phi)=N.$
2. It is satisfied that $G=NH$ and $H\cap N=\{e\}.$
When any of those requirements is satisfied we write
$$ G=N\rtimes H $$$\blacksquare$
Definition
When we have the context given by condition 1 or 2 we say that $G$ is the semidirect product of $N$ and $H$ and we write $G=N \rtimes H$.
$\blacksquare$
Remarks
- The "converse" is not true. Given a normal subgroup $N$ of $G$, $G$ is not necessarily the semidirect product of $N$ and $G/N$. For example: $\mathbb Z/4\mathbb Z$ which contains $\mathbb Z/2\mathbb Z$. I have to think it.
- Another characterization. An exact sequence $0 \rightarrow N \rightarrow G \rightarrow H \rightarrow 0$ to be isomorphic to one of the form $0 \rightarrow N \rightarrow N \rtimes H \rightarrow H \rightarrow 0$ is if $G \rightarrow H$ has a section.
- Here $NH$ must not be confused with $N\times H$, the direct product (see product (cat th)). Instead, is a product of group subsets,
- Under condition 2 every $g\in G$ can be written in an unique way as a product $g=nh$, $n\in N, h\in H$. If $nh=n'h'$ then $(n')^{-1}n=h'h^{-1} \in N\cap H$ and therefore $(n')^{-1}n=h'h^{-1}=e.$
- Condition 1 is like saying that the main group $G$ can be seen like a bundle, since we have a idempotent map $\phi: G \rightarrow H$. The standard fibre is $N$.
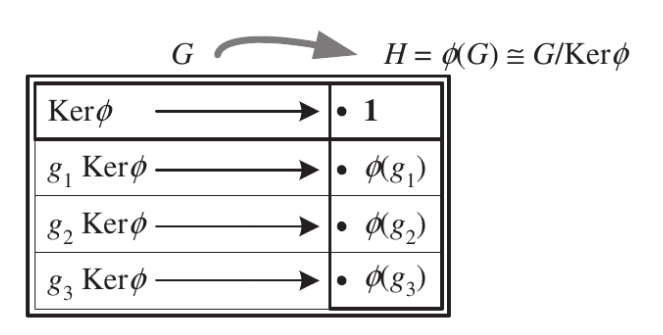
Image from Mathematics for Physics, an ilustrated handbook, page 40.
Proof
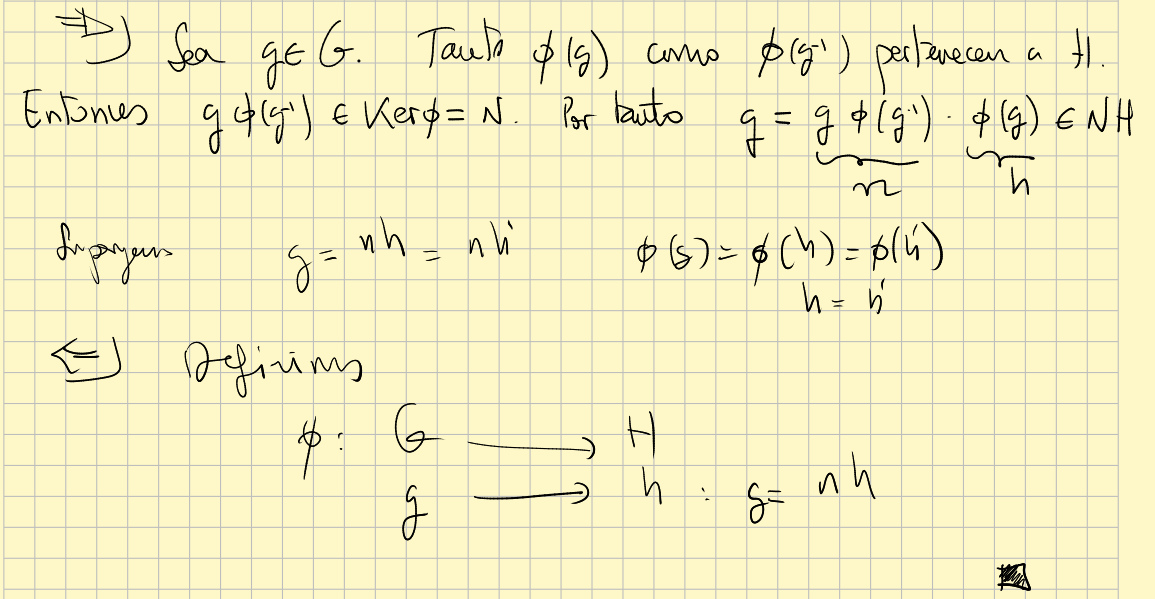
$\blacksquare$
The product in $G$
The product in $G$ takes a special form: given $g=(n,h)$ and $g'=(n',h')$ then $gg'=(\bar{n},\bar{h})$ and
$$ \bar{n}\bar{h}=nhn'h'=nhn'h^{-1}hh' $$therefore
$$ \bar{h}=hh' $$ $$ \bar{n}=nhn'h^{-1} $$We can think in $N$ as translations and $H$ as rotations.
Key example
Suppose the group $E(2)$ of isometries of the euclidean plane, or rigid motions. It is known that any element of $E(2)$ can be seen as the composition of a translation (an element of $\mathbb{R}^2$) and a linear isometry (an element of $O(2)$, that is, a rotation with centre at the origin or a reflection with axis through the origin). This decomposition is unique.
Moreover, translations are a normal subgroup of $E(2)$: you can see it intuitively "moving things on a table" or by computation:
$$ v\mapsto R(R^{-1}v+t)=R R^{-1}v+Rt=v+Rt $$Therefore
$$ E(2)=\mathbb{R}^2 \rtimes O(2). $$In general, if we now consider any subgroup $H$ of $GL(n)$ we can consider the subgroup $G$ of $GL(n+1)$
$$ G=\left\{\begin{pmatrix} B & v\\ 0 &1\\ \end{pmatrix}:B\in H, v\in \mathbb{R}^n \right\} $$It is easy to show that $G$ is isomorphic to $\mathbb{R}^n \rtimes H$ (construct the map $\phi$ of the definition).
Conversely, given any group $G=N\rtimes H$, with $N\approx \mathbb{R}^n$ and $H\approx \tilde{H}\leq GL(n)$, it can be shown that $G$ is isomorphic to a subgroup of $GL(n+1)$ of this form. Consider
$$ \bar{N}=\left\{\begin{pmatrix} I & v\\ 0 &1\\ \end{pmatrix}:v\in \mathbb{R}^n \right\} $$and
$$ \bar{H}=\left\{\begin{pmatrix} B & 0\\ 0 &1\\ \end{pmatrix}:B\in \tilde{H}\right\} $$Now it is easy to see that $G$ is isomorphic to a subgroup of $GL(n+1)$ with the form above by means of the map:
$$ \varphi: G=N\rtimes H \to\bar{N}\times\bar{H} \to GL(n+1) $$ $$ (n,h)\mapsto \left(\begin{pmatrix} I & v\\ 0 &1\\ \end{pmatrix},\begin{pmatrix} B & 0\\ 0 &1\\ \end{pmatrix}\right) \mapsto \begin{pmatrix} B & v\\ 0 &1\\ \end{pmatrix} $$This map is a homomorphism. The product in $G$ takes the form
$$ (n,h)(n',h')=(nhn'h^{-1},hh') $$and with a standard computation can be checked that
$$ \varphi((n,h))\cdot \varphi((n',h'))=\varphi((nhn'h^{-1},hh')) $$Moreover, the map is also injective, as it is easy to check.
Another approach
Within this approach we can create a group being the semidirect product of two given groups.
Definition. Let $H$ and $N$ be groups, and let $\phi: H \rightarrow \text{Aut}(N)$ be a group homomorphism such that $\phi(h)$ defines a group action of $h$ on $N$. The semidirect product $N \rtimes_{\phi} H$ is the Cartesian product $N \times H$ endowed with the multiplication operation
$$ \cdot : (n, h) \cdot (n', h') = (n \phi(h)(n'), hh') \quad \forall n, n' \in N, \, h, h' \in H, $$where $\phi(h)(n')$ denotes the action of $h$ on $n'$.$\blacksquare$
It can be shown that it is indeed a group.
About the Lie algebras
I think it can be proven the following proposition
Proposition
Let $G$ be a Lie group that is the semidirect product of a normal subgroup $N$ and a subgroup $H$, i.e., $G = N \rtimes H$. Then the Lie algebra $\mathfrak{g}$ of $G$ has a canonical decomposition as an $Ad(H)$-module given by
$$ \mathfrak{g} = \mathfrak{n} \oplus \mathfrak{h}, $$where $\mathfrak{n}$ and $\mathfrak{h}$ are the Lie algebras of the subgroups $N$ and $H$, respectively.$\blacksquare$
Proof
The idea is:
- Show that $\mathfrak{g} = \mathfrak{n} \oplus \mathfrak{h}$ as vector spaces
- $\mathfrak{g}$ is an $Ad(H)$-module, and of course $Ad(H)(\mathfrak{h})\subset\mathfrak{h}$. But also, since $N$ is normal, we have that $Ad(H)(\mathfrak{n})\subset\mathfrak{n}$
$\blacksquare$
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: